
Summary
We present a stochastic differential equation (SDE) approach for general-purpose image restoration. The key construction consists in a mean-reverting SDE that transforms a high-quality image into a degraded counterpart as a mean state with fixed Gaussian noise. Then, by simulating the corresponding reverse-time SDE, we are able to restore the origin of the low-quality image without relying on any task-specific prior knowledge. Crucially, the proposed mean-reverting SDE has a closed-form solution, allowing us to compute the ground truth time-dependent score and learn it with a neural network. Moreover, we propose a maximum likelihood objective to learn an optimal reverse trajectory which stabilizes the training and improves the restoration results. In the experiments, we show that our proposed method achieves highly competitive performance in quantitative comparisons on image deraining, deblurring, and denoising, setting a new state-of-the-art on two deraining datasets. Finally, the general applicability of our approach is further demonstrated via qualitative results on image super-resolution, inpainting, and dehazing.
Forward SDE for Image Degradation
$dx = \theta_t \, (\mu - {x}) dt + \sigma_t dw$
Reverse-Time SDE for Image Restoration
$dx = \big[ \theta_t \, (\mu - x) - \sigma_t^2 \, \nabla_x \log p_t(x) \big] dt + \sigma_t d\hat{w}$
Illustration of Image Restoration Process
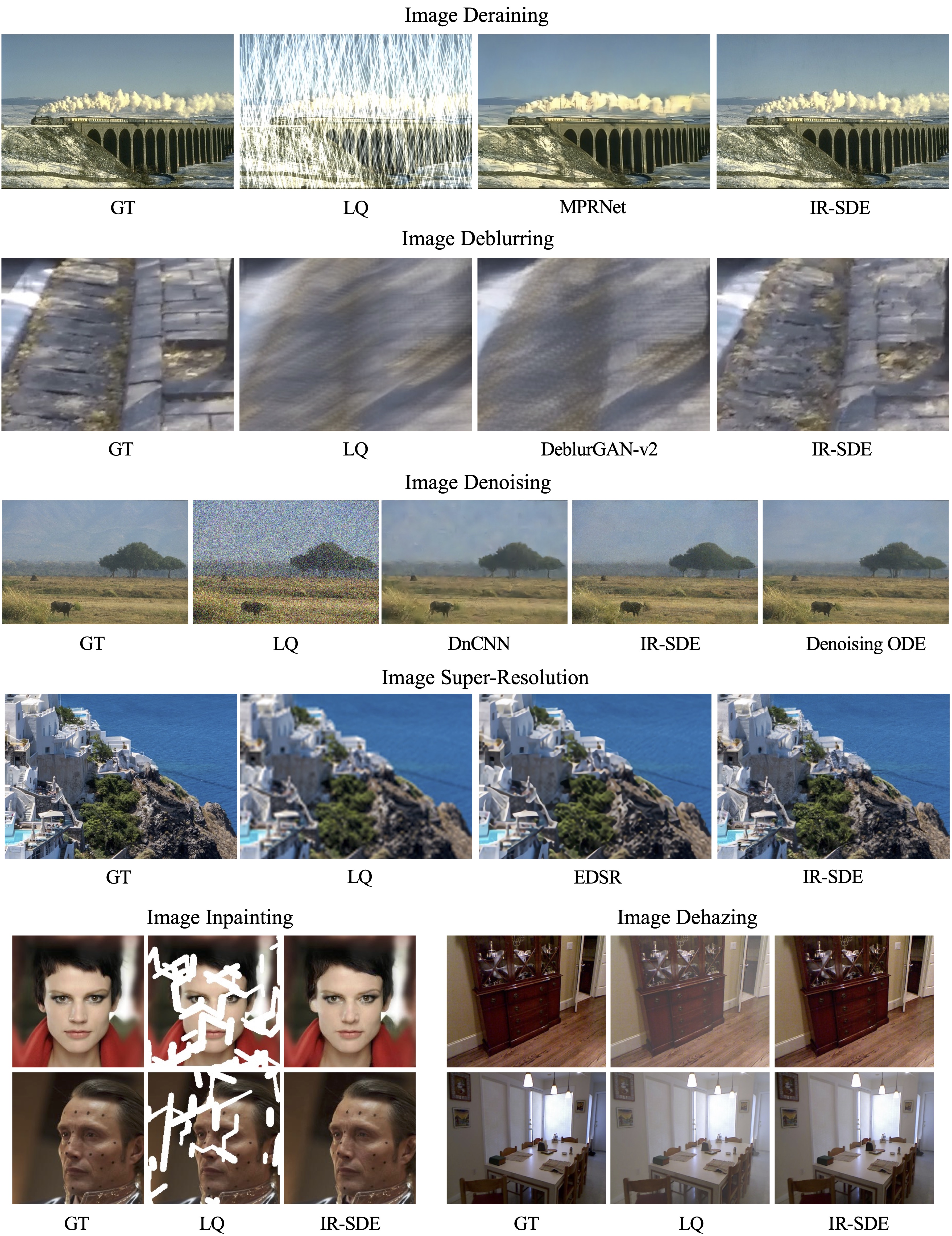
We experimentally evaluate our proposed IR-SDE method on several popular image restoration tasks: image deraining, deblurring, denoising, super-resolution, inpainting, and dehazing. Our method doesn't need to known any prior of the degradation, and the only change required for each task was to change the dataset. Below we visually illustrate the reverse-time process of the IR-SDE on different tasks.
Image deraining
Image denoising
Interpolation
With IR-SDE, we can also perform interpolation by letting source image to be $x(0)$ and target image to be $\mu$, and then simply simulating the forward SDE process.
Image Interpolation
Related Projects
- This template is built upon SR3: Image Super-Resolution via Iterative Refinement.
Citation
@article{luo2023image,
title={Image Restoration with Mean-Reverting Stochastic Differential Equations},
author={Luo, Ziwei and Gustafsson, Fredrik K and Zhao, Zheng and Sj{\"o}lund, Jens and Sch{\"o}n, Thomas B},
booktitle={Proceedings of the 40th International Conference on Machine Learning},
pages={23045--23066},
publisher={PMLR},
year={2023}
}